常规的压力容器设计是按规范(例如我国的GB 150《钢制压力容器》规范)设计。它实际上是以弹性失效为设计准则，因此计算与分析都是比较简单的，但也潜在着一定程度的盲目性。
       随着生产发展和科学技术水平的不断提高，容器的建造向大型化方向发展，按规范进行压力容器的设计的缺点和局限性越来越显露出来。人们开始研究并出现了按全面的应力分析进行设计的方法，即“分析设计”法。分析设计是根据具体工况，进行详细的应力计算与分析。其理论基础是板壳力学、弹性与塑性理论及有限元法。其优点表现在：1)考虑了超出弹性范围以后结构的塑性行为，放弃传统的弹性失效准则。引入极限分析与安定分析概念，采用塑性失效设计准则。2)应用数值分析和实验测试技术，对复杂结构的容器整体，包括任何不连续区域都可以做详细的应力分析与计算。3)按不同性质的应力分类和失效形式给予不同的限制条件。但要实现设计上的安全可靠必须遵循相应的规范。目前，我国分析设计的容器规范是文献。
      本文讨论的内压圆筒上开有大的矩形孔，孔的轴向长度/圆筒的轴向长度大于0. 5，已不适宜应用GB 150《钢制压力容器》规范，而应按照文献进行强度CAE分析。
      按照压力容器分析设计规范，对于受内压的筒体及加强座结构，其应力类型主要有：一次总体薄膜应力(代号P)，一次局部薄膜应力(代号Pl)，一次弯曲应力(代号Pb)，二次弯曲应力(代号Q)和峰值应力(代号F)。对于不同类型的应力应给予不同的许用极限加以限制。为了从有限元分析结果中得到薄膜、弯曲和峰值等应力，一般采用点处理法和线处理法。
      采用点处理法对一个点的应力强度进行评定是最简单的方法，相对而言也是不准确的方法，往往会掩盖潜在的危险。而线处理法是较新的应力强度评定方法，它主要是利用沿壁厚的一条线的三维有限元应力值进行拟合，依据“静力等效”和“静弯矩等效”的原理分离出均布应力和弯曲应力，进而计算出各类应力。
      压力容器分析设计规范规定的材料设计许用应力。两式中的最小值，几是常温下材料的最低屈服极限和最低抗拉强度。国标规定的安全系数为n，它们是在总结以往使用经验和参考国外同类标准以后规定的。取上述最小值的意义，是既要按1.5保证处于弹性状态，控制塑性失效，又需防止发生断裂爆破。这不仅有利于提高设计许用应力，而且又不失安全性。
      综上所述，文献选取的安全系数值为：
      n=1.5，n1=2.6(在常温下)，
      对于应力强度分析需要评定以下各种应力：
      1)总体一次薄膜应力S1得到少，
      2)局部一次薄膜应力S2由P得到少，
      3)一次加二次应力S3(由PL+Q得到)，
      4)峰值应力S4(由P+Q+F得到)。
      各种应力的限制条件不大于材料的许用应力S或其一定倍数。根据规范要求：总体一次薄膜应力Si，局部一次薄膜应力Sz，一次加二次应力S3<S5，峰值应力的许用极限由疲劳曲线得到的许用值进行评定。压力容器上加强座材料的a=225 Mpa，故Sr=225/1.5=150 Mpa。
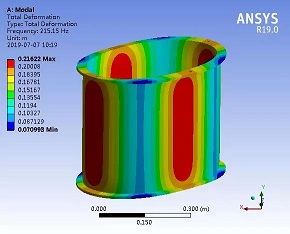
      所分析的压力容器所受的载荷具有轴对称性。对大开孔中心所在的横剖面，结构的应力状态是对称的。另外，对大开孔中心所在的纵剖面，结构的应力状态也是对称的。因此，本分析计算取筒体结构的八分之一建立模型和划分网格，具体模型见图。

                                                                                专业从事机械产品设计│有限元分析│CAE分析│结构优化│技术服务与解决方案
                                                                                                                                                      杭州那泰科技有限公司
                                                                              本文出自杭州那泰科技有限公司www.nataid.com，转载请注明出处和相关链接！